Chapter 7 – Arrays and Pointers

(Updated May 19, 2023)

Table of contents

Overview
Arrays
Pointers
Dynamic Arrays, Initialization and length
Variable Length Arrays (VLAs)
Array Processing
Copying Arrays
Arrays of Objects
Variable Length Parameter List
Two-Dimensional Arrays
Review
Summing Arrays
Managing Arrays
Quiz
Exercises

Overview

In the past, when calculating an average, we could sum up values entered by the user (or read from a file) and produce a precise result. Usually, the need for historic information was unnecessary, and we added the new value to the running total and retrieved the next value from the source.

In other words, we set up a loop to get a value, add it to the running total, toss it, and fetch the next one.

Arrays help to address an issue with the longevity of data. We often use the terms short-lived and long-lived. Up to this point, our data has been relatively short-lived. But arrays are not just tools to help data live longer.

Now, what if you need to also use that data for some other purpose that is unrelated to calculating an average? Well, you could create a variable for every value you know you will read from the user, such as:

int test1, test2, test3;

But what if there are 5 test grades? What if 100 integer values needed to be long-lived? What if you did not know until runtime when the user tells you how many?

Arrays also solve the problem of how to store our long-lived data efficiently.

Arrays

As the amount of long-lived data increases, we can easily make an argument for an alternative data structure that allows us to:

• Collect related same-typed data together.
• Identify the values with a common name.
• Allow (potentially) an unlimited number of items in the collection.

An array achieves exactly that. We can put many items of the same type into a single variable
name and address each item uniquely. These one-dimensional arrays allow us to keep a
linear collection of data. Now let us make some arrays!

Array declarations are made like so:

int array[10];

But can also be declared as:

int *array;

The former indicates that the variable is declared an array of pre-allocated storage of a specific size with uninitialized data. In contrast, the latter says that array is a pointer to int – possibly many ints – and the storage has not yet been allocated.

char *s = "Some text.";

char s[] = "Some text.";

#include <stdio.h>

int main(int argc, char *argv[]) {
  
  char *s = "Some text.";  
  char t[] = "Some text.";
  
  printf("%2lu %p\n%2lu %p\n", sizeof s, s, sizeof t, t);
}

Using the original example of a 10-element int array:

int array[10];

By default, arrays in C are uninitialized. Let us see just what the array looks like.

Figure 1: Newly created 10-element integer array.

Figure 1 shows how the array is arranged in memory. We can store 10 integers in the array. However, this is uninitialized memory which is why we have question marks in those spaces.

Each element in the array is numbered with an index value. This index value will allow us to address each element individually. We uniquely identify each element with the array’s name followed by the index value in square brackets ([ ]). So the first element is array[0], the second element is array[1], and the tenth and final element is array[9].

Figure 2: The array after altering two elements.

Figure 2 shows the array modified by placing the specifically named element on the left of an assignment operator with the following statements:

array[1] = 56;
array[6] = 23;

The square brackets ([ ]) are known as the array subscripting operator. This operator allows us to inspect or modify an element of an array. So the first statement says, “The element at index 1 gets the value of 56,” while the second statement says, “The element at index 6 gets the value of 23.” Remember that array[1] is the second element of the array.

When the time comes to access existing values, we use the same nomenclature. For example, the following statement prints the value of the third element of the array whose value is presently zero:

printf("The value of array[2] is %d\n", array[2]);

Generally, arrays are pretty simple to work with. It’s a pile of data in a neat little package.

Pointers

At this stage, pointers are not a new thing. We have used the address-of operator (&) to obtain the address of a variable for use with functions like scanf. So, we know pointers exist and that we do very powerful and bad things with them.

We saw them in Chapter 6 when we were trying to change values in arguments.

This section helps to clarify some details about pointers.

• Pointers are not arrays. Although we can use array notation with them.
• Pointers can traverse memory in ways not available to arrays.
• Pointers are uninitialized, and we must assign them something to point to.
• Pointers are essential for managing dynamic memory and creating data structures.
• Misused pointers can lead to computational errors, data corruption, and program failure.

We have so much power, so let’s see what we can do.

Dynamic Arrays, Initialization and length

Now consider:

int *array;

Of course, this only declares a pointer variable. This array variable is a pointer to memory that will hold several values you request. As such, we are required to use the malloc function to get the space, so if we needed a 10 integer array, or rather an array with 10 integer elements, we could do one of the following:

int *array = malloc(10 * sizeof(int));

or

int *array;
array = malloc(10 * sizeof(int));

Ideally, we want to test the value returned by malloc and confirm that it is not a null pointer. If a null pointer is returned, we have most likely exhausted memory in the heap. The heap is where we get dynamic runtime storage. We can allocate space with malloc() (and calloc()), but remember that we have to return the memory when we’re done with free().

Arrays may also be initialized during declaration by specifying a set of initial values in braces ({ }) such as:

int initializedArray[] = {53, 0, 26, 17, ­5, 22};

The initalizedArray variable declaration implies a new int[6] and sets the initial values of the array. The new operator is not explicitly used since it is implied, and the number of initial values determines the array size. At runtime, your array will be of the implied length and contain those specified values.

Other forms of initialized arrays are shown below.

int array1[] = {3, 6, 8};     // array of length 3.
int array2[20] = {8, 27, 10}; // array of length 20 with 3 values and the rest zeroes.
int array3[10] = {0};         // array of length 10 with 10 zeroes.

Variable Length Arrays

What is particularly interesting about C arrays is the ability to specify the array size at runtime know as variable length arrays or VLAs. VLAs came about in the C99 standard.

Let us say we need the user the tell us how many integers to maintain. The following piece of code is a good place to start:

int size;
printf("Enter length of array: ");
scanf("%d", &size);

int ia[size];

printf("%lu %p\n", sizeof ia, ia);

The value of size, which is input by the user, is used to allocate the array dynamically to make sure the array size is precise.

Sample output is shown below where the address confirms the use of the stack as automatic storage.

Enter length of array: 10
40 0x7ff7b2e7f120

There are a few things to note about the use of VLAs:

• The space is allocated on the stack and NOT the heap. Therefore the memory is not returned through free.
• The declaration of the array MUST appear after you know the size.
• If the array is declared inside a loop construct, the array will be allocated each time the statement is encountered in the loop.
• The array’s lifetime is only until the variable goes out of scope. If this is allocated in a function, you must copy that data before leaving if you intend to keep it. The stack contents will be purged upon exit of the function.
• Consider all of your options before choosing a VLA.

Array Processing

#include 
#include 
#include 

void printArray(int a[], int l) { 
  int x; 
  for (x = 0; x < l; x++)
    printf("Value at index %d is %d\n", x, a[x]);
} 

int main(int argc, char *argv[]) {
  int array[5]; 
  int len, x, sum=0; 
  double avg; 
  
  len = sizeof array / sizeof array[0]; 
  
  // initialize the array to random numbers. 
  for (x = 0; x < len; x++) 
    array[x] = rand() % 100 + 1; 
  
  // display array contents. 
  printArray(array, len); 
  
  // read data into array. 
  for (x = 0; x < len; x++) {
      printf("Enter value for array[%d]: ", x); 
      scanf(" %d", &array[x]); 
  } 
  
  // display array contents. 
  printArray(array, len); 
  
  // sum the array and calculate the average. 
  for (x = 0; x < len; x++) 
    sum = sum + array[x]; 
  avg = (double)sum / len; 
  
  printf("The average of the entered values is %.2f\n", avg); 
}

Example 1: Program demonstrating array processing.

The program in Example 1 shows many programmatic methods to handle the processing of arrays, such as setting random values, displaying the elements, assigning values from user input, building a sum, and calculating an average.

Note that for each processing method, we are usually altering or inspecting every element of the array. This indicates that a loop is essential. Why? We have to perform the same work on each array element. Recall that our iterative constructs are the best tools we have for performing the same work a certain number of times, especially with related data.

Note that for each loop we construct to process the array we are always using the range of [0..length-1], that is we are starting at zero and stopping at the last element which is length minus one. Starting at zero makes sense, of course, since we know that array indexes start at zero. The use of the operator < rather than <= is important as well. Not only does this clearly allow us to say length-1 by way of stating x < len, but we must be careful of a runtime fault.

A runtime fault indicates that something has caused the program to crash. Note that in Example 1, the variable x is being used as the index to visit each element and either inspect or alter the current value. If x < 0 or x >= len, the index is out of bounds, and the program could crash with a segmentation fault. This is due to C not having array bounds checking by default. Some compilers allow you to add compiler switches that will add code for bounds checking.

len = sizeof array / sizeof array[0];

Here is a sample run of array_proc from Example 1:

Value at index 0 is 79 
Value at index 1 is 36 
Value at index 2 is 73 
Value at index 3 is 74 
Value at index 4 is 11 
Enter value for array[0]: 45
Enter value for array[1]: 20
Enter value for array[2]: ­9
Enter value for array[3]: 4875
Enter value for array[4]: 38
Value at index 0 is 45 
Value at index 1 is 20 
Value at index 2 is ­9 
Value at index 3 is 4875 
Value at index 4 is 38 
The average of the entered values is 1656.33 

The first set of values displayed are the random numbers, followed by the set of prompts for the user to enter values (shown in bold). The values of the array are displayed again showing the user supplied valued and finally, the average is calculated and displayed.

The method printArray() is used to display the contents of the array without repeating the code to do so – which is, of course, one of the reasons we use methods. This method demonstrates the ability to declare arrays as formal parameters and also demonstrates passing array parameters.

It is important to realize that although we have the length instance variable within the array object to tell us the number of elements, there is the possibility that we may not be using all of them. In this case, we should consider overloading the printArray() method like so:

public static void printArray(int[] a, int num) 
{ 
   int x;
   for (x = 0; x < num; x++) 
   { 
      System.out.println("Value at index " + x + " is " + a[x]); 
   } 
    
} 

Copying Arrays

Arrays of information are often duplicated when it is necessary to keep an original view of the data prior to altering it for some other purpose. Consider the following:

int[] ia1 = {10, 20, 30, 40, 50};
int[] ia2 = new int[ia1.length];

We have created ia1 as an initialized array and ia2 as a new array whose length matches ia1. You may fall for the trap of trying the following:

ia2 = ia1;

But if you remember the issue of shallow versus deep copying with objects, then you should immediately recall that this will only lead to ia2 referencing the same memory as ia1 – clearly not a copy of ia1.

We can perform the deep copy a few ways. Since ia2 has already been instantiated, we can use a loop like the following:

int x;
for ( x = 0; x < ia1.length; x++ )
  ia2[x] = ia1[x];

We can also us the arraycopy() static method of the System class like so:

System.arraycopy(ia1, 0, ia2, 0, ia1.length);

The arraycopy() method takes as arguments the source array, source array starting index, destination array, destination array starting index and the number of elements to copy. This particular call is stating that we should copy ia1.length characters from ia1 starting at ia1[0] into ia2 starting at ia2[0].

If there was no instantiated object for ia2 or we no longer cared about one that was, we could do something like:

ia2 = (int[])ia1.clone();

The clone() method is available since arrays implement the Cloneable interface. Note that the clone() method returns an Object type that needs to be cast to an integer array. The cloned array is new instance and therefore a deep copy.

Beginning at JDK 6 there is yet another method by which we can copy arrays. In the Arrays class of the java.util package, there is a static method called copyOf(). This may seem odd to have yet another method of copying arrays, but this method also solves the problem of what to do about the fact that arrays cannot be lengthened. Using the copyOf() method we can specify a length for the new array which can be longer than the source array. We can copy the contents of ia1 into a new array that is twice the length of ia1. The variable ia2 will reference an array twice the size of ia1 with the following code:

ia2 = Arrays.copyOf(ia1, ia1.length * 2);

The contents of the object referenced by ia2 will be the exact copied values from the elements of ia1 followed by zeros in the remaining elements as shown in Figure 3.

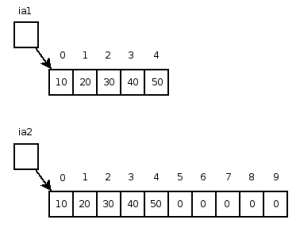
Figure 3: Arrays after a call to copyOf().

Example 2 shows code implementing all four methods for copying arrays.

import java.util.Arrays;

public class ArrayCopy 
{ 
   
   public static void resetArray(int[] a) 
   { 
      int x; 
      for ( x = 0; x < a.length; x++) 
        a[x] = 0; 
   } 
   
   public static void printArray(int[] a) 
   { 
      int x, len = a.length; 
      for (x = 0; x < len; x++) 
      { 
         System.out.println("Value at index " + x + " is " + a[x]); 
      } 
      
   } 
   
   public static void main(String[] args) 
   { 
      int[] ia1 = new int[5]; 
      int[] ia2 = new int[5]; 
      int x; 
      
      // initialize the array to random numbers. 
      for (x = 0; x < ia1.length; x++) 
      { 
         ia1[x] = (int) (Math.random() * 100 + 1); 
      } 

      // display array contents. 
      System.out.println("\nContents of ia1"); 
      printArray(ia1); 
      
      // deep copy ia2 into ia1 with for loop 
      System.out.println("\nUsing for loop"); 
      for (x = 0; x < ia1.length; x++) 
        ia2[x] = ia1[x]; 
      
      printArray(ia2); 

      // deep copy with arraycopy() 
      resetArray(ia2); 
      System.out.println("\nUsing System.arraycopy()"); 
      System.arraycopy(ia1, 0, ia2, 0, ia1.length); 
      printArray(ia2); 
      
      // shallow copy ia2 to ia1 
      System.out.println("\nBefore shallow copy"); 
      System.out.println("ia1 hash = " + System.identityHashCode(ia1)); 
      System.out.println("ia2 hash = " + System.identityHashCode(ia2)); 
      
      ia2 = ia1; 
      System.out.println("\nAfter shallow copy"); 
      System.out.println("ia1 hash = " + System.identityHashCode(ia1)); 
      System.out.println("ia2 hash = " + System.identityHashCode(ia2)); 

      // Use Arrays.copyOf() ­ JDK 6 
      System.out.println("\nUsing Arrays.copyOf() with ia1.length*2"); 
      ia2 = Arrays.copyOf(ia1, ia1.length * 2); 
      printArray(ia2); 
      
   } 
} 

Example 2: Program showing the various methods of copying arrays.

Arrays of Objects

The best example of an array of objects is the args formal parameter when you declare the main() method as demonstrated here:

public static void main(String[] args)
{
  int x;
  for (x=0; x < args.length; x++)
    System.out.println("args[" + x + "] = " + args[x]);
}

At this point it should be fairly evident that args is an array of String objects. This implies that there is also a length instance variable and that we could display all of the element values as is further demonstrated with the for loop in the main() method.

Of course the next logical question is how did the values get into the args array? The args array is populated at runtime when your Java program is invoked. From the Unix command line it might be something like:

$ java myProgName argument1 "Argument 2" arg3

There are three arguments passed and args.length will reflect this particular fact. Note the
double quotes around the second argument. This is a common feature of an operating system command line interface to allow the use of quotes when there is a need for embedding spaces. Otherwise we see that the arguments are separated by the use of the space characters.

It is important to remember that args is a reference variable of an object that is a String[] and that args[0] is a reference variable of a String object. Figure 4 helps to put this picture into perspective.

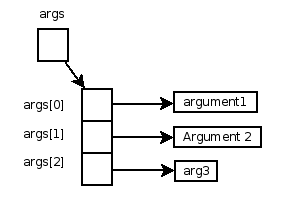
Figure 4: Memory layout of args parameter.

You may be using a product such as DrJava or other such IDE (Integrated Development Environment). Figure 5 shows a way to have command line arguments passed to your Java program.

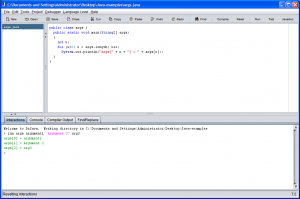
Figure 5: How to pass arguments in DrJava.

Variable Length Parameter List

Recall the method printf() and its seemingly unending number of parameters we may pass to it. As printf() was new with JDK 5, so was this particular concept of having a variable length parameter list. Simply put you can create a method with an unknown number of parameters and Java will adjust. What is actually happening is Java is coalescing the parameters into an array that the method can access through an array formal parameter.

The rules governing variable length parameter lists are as follows:

• You can combine both variable length formal parameters with other formal parameters.
• Variable length formal parameters may be a primitive type or comprised of objects.
• A method can have at most one variable length parameter list.
• The variable length formal parameter must be the last formal parameter of the formal parameter list.

If you wanted a method to accept any number of integers when used in a Java program you could declare something like:

public static int sum(int ... integers)
{
  // other statements
}

This declaration says that sum is a method that returns an int and integers can be an as yet unnumbered set of parameters. The ellipsis (...) indicates the we do not know how many integers might be passed to this method. We can process this unnumbered set as an array in a couple of ways. This first version allows us to use the standard for loop as we have been doing it:

public static int sum(int ... integers)
{
  int x, total=0;
  for (x = 0; x < integers.length; x++)
    total = total + integers[x];
  return total;
}

As you can see the only real detail to mention here is that although the integers declaration has no brackets ([ ]) we are still processing the contents as an array. An alternative to this level of detail with loop control based on the index value of the array is to use what is known as a foreach loop. It simply allows us to declare a single variable that will receive the next value from the array without having to use a variable to keep track of the index. We can rewrite the previous example to demonstrate:

public static int sum(int ... integers)
{
  int total=0;
  for (int item : integers)
    total = total + item;
  return total;
}

The specific detail of the foreach loop is highlighted. It is still a for loop, but with a change to its parenthetic contents. We substitute an iterator, namely item, to represent the first and subsequent elements of the integers array. Keep in mind that you have no direct knowledge of the index value of item with each iteration.

Since foreach loops are powerful and lead to simpler looking code, they are often used for Vectors and other iterable collections as we will see later.

Two Dimensional Arrays

Up to this point all of our arrays have been one-dimensional arrays. Clearly more dimensions would be advantageous, but how far do you take these dimensional components? Two? Three? More?

Let us consider for a moment a game of tic-tac-toe. Do not imagine rules or strategy, just imagine the board. That simple 3x3 game board. This can be represented in a two dimensional array. Once you've conceived that notion, you can immediately see how the game board used for checkers and chess swiftly becomes an 8x8 two dimensional array. Let's declare our game boards:

char[][] tictactoe = new char[3][3];
int[][] chess = new int[8][8];

The type for each board could certainly be debated, but for now let us just look at the layouts of these boards in memory as shown in Figure 6.

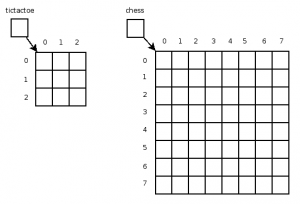
Figure 6: Memory layouts for tictactoe and chess.

With our one-dimensional arrays, we could draw the array horizontally and call each element a column, or draw it vertically and call each element a row. Of course, neither makes sense in a one-dimensional world. Move to a two-dimensional world and now we must know which index value represents rows and which is the column index value. The first dimension always represents the row and the second dimension is the column. This applies to the declarations as well. The first bracketed value represents the number of rows and the second bracketed value is the number of columns.

Just as with one-dimensional arrays, we can initialize two-dimensional arrays. The following code piece demonstrates how to do this:

int[][] threebythree = {{1, 2, 3},
                        {4, 5, 6},
                        {7, 8, 9}};

This is a three by three array which is instantiated and initialized for us. Recall that with initial values specified, we do not use the new operator.

Of course, Java also allows for what is known as ragged arrays. Ragged arrays are multiple one-dimensional arrays collected into a two-dimensional framework. Consider for a moment that we would like a three row array with five elements in the first row, two elements in the second row and four elements in the third. The following declarations create just that:

int[][] ragged;         // declare two­dimensional array
ragged = new int[3][];  // create three rows
ragged[0] = new int[5]; // create first row of 5 elements
ragged[1] = new int[2]; // create second row of 2 elements
ragged[2] = new int[4]; // create third row of 4 elements

At first glance one may wonder how to handle the processing of such arrays, but remember that each array is an object and there exists an instance variable length for each array. With that knowledge alone, you can process any array layout.

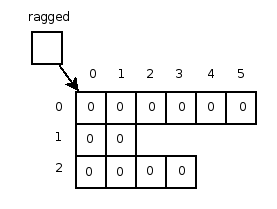
Figure 7: Two­dimensional array with"ragged" rows.

The diagram in Figure 7 depicts our ragged array. The code in Example 3 shows some methods of processing two-dimensional arrays and are generic enough for both equal length rows and ragged arrays.

The class array2dproc in Example 3 creates a randomized ragged array of between 2 and 10 rows and each row will have between 2 and 10 columns. In addition as with Example 1 we have randomized the values within the two-dimensional array. The user input has been removed from this example. Recall that printArray() in Example 1 was used to display the contents of the array. In this version we have adapted it to print any two-dimensional
array.

import java.util.Scanner; 

public class Array2DProc 
{ 
   
   static Scanner kb = new Scanner(System.in); 

   public static void printArray2d(int[][] a) 
   { 
      int row, col; 
      for (row = 0; row < a.length; row++) 
      { 
         System.out.print("Values in row " + row + ": "); 
         for (col = 0; col < a[row].length; col++) 
           System.out.printf("%3d ", a[row][col]); 
         
         System.out.println(); 
      } 
   } 
   
   public static void main(String[] args) 
   { 
      int[][] array; 
      int row, col, x; 
      double avg, sum; 
      
      x = (int)(Math.random() * 9 + 2); 
      System.out.println("\nCreating ragged array of " + x + " rows"); 
      System.out.println("Each row length between 2 and 10 integers.\n"); 

      // create x rows 
      array = new int[x][]; 

      // create x columns for each row 
      for (row = 0; row < array.length; row++) 
      { 
         // range 0 through 8 + 2 yields 2 through 10 
         x = (int)(Math.random() * 9 + 2); 
         System.out.println("Row " + row + " is " + x + " integers long."); 
         array[row] = new int[x]; 
      } 
      
      // initialize the array with random numbers. 
      System.out.println("\nInitializaing each row with random numbers."); 
      for (row = 0; row < array.length; row++) 
         for (col = 0; col < array[row].length; col++) 
           array[row][col] = (int) (Math.random() * 100 + 1); 

      // display array contents. 
      printArray2d(array); 
      
      // sum the array and calculate the average. 
      System.out.println("\nCalculating average of each row."); 
      for (row = 0; row < array.length; row++) 
      { 
         sum = 0.0; 
         for (col = 0; col < array[row].length; col++) 
           sum = sum + array[row][col]; 
         avg = sum / array[row].length; 
      
         System.out.printf("The average of row %d is %.2f\n", 
                           row, avg); 
      } 
   } 
}

Example 3: Program to demonstrate processing of two-­dimensional arrays.

We will begin with the main() method and discuss the details. First we generate a random number between 2 and 10. This value is used to specify the number of rows in the ragged array. Once that value is calculated, we inform the user of the number of rows, create the rows and assign them to array.

Next a for loop is employed to generate a set of randomized values representing the number of columns in each row. For each row iteration we generate a new value between 2 and 10 and create a new array of length x and assign it to array[row].

The subsequent block of code uses a nested loop to populate the array with random numbers in the range 1 through 100. The outer loop iterates through the rows of the ragged array while the inner loop iterates each column of a given row. Note that all iterations of the inner loop must complete prior to the next iteration of the outer loop. In this way we enable the processing of each row one after another.

When we have finished populating the array, we call the printArray2d() method to display the contents of the array. We will discuss printArray2d() in a moment.

The final block of code employs another nested loop to average the values in each row of the ragged array. For each row we initialize the sum to zero, calculate a total for the values in the row using the inner loop, calculate the average and display the row average. Each row is calculated in this way for each iteration of the outer loop.

Now back to printArray2d(). This method demonstrates passing a two-dimensional array parameter. It also demonstrates how to establish generic criteria for array processing. Since we have no knowledge of the array size or whether the array rows are equal length or ragged, the method has been constructed to always use the number of rows (a.length) and the number of columns (a[row].length). In this way we will not complicate the method with additional parameters such as rows and columns which would complicate our ability to process ragged arrays to be certain.

On a final note, ragged arrays certainly are special purpose arrays and are not likely to grace your code often. They do however demonstrate the need to consider the possibility that data values by nature are often incomplete or asymmetric.

Review

Recall that arrays address a need to keep multiple pieces of related data in flight. Thought some clever packaging, we can reduce the storage footprint by using a single name to represent many values rather than having one variable for each value. This simplifies data management, especially parameter passing.

When passing arrays to a method we only need to pass one name for all the values. Since arrays already have a length associated with the content, no additional information is required. However, if we are not using the total amount of space allocated for the array, we need to keep track of how much is actually in use. Failing to do this will result in errors in our calculations.

Summing Arrays

Arrays are quite versatile, but also require significant responsibility. Consider summing the contents of an array. There are two basic ways to handle the contents of the array. We have the opportunity to use the entire allocated space of the array, basically implying the array is always at full capacity. The other option is to only use a portion of the array. No one method is necessarily better. It becomes a choice of how to handle our data.

public class UsingArrays1 {
  
  // Sum all values in array.
  public static int sum(int[] array) {
    
    int x, sum = 0;
    
    for ( x = 0; x < array.length; x++)
      sum = sum + array[x];
      
    return sum;
  }
  
  // Sum all the values inuse in array.
  public static int sum(int[] array, int inuse) {
    
    int x, sum = 0;
    
    for ( x = 0; x < inuse; x++)
      sum = sum + array[x];
      
    return sum;
  }
  
  public static void main(String[] args) {
  
    int x, ia[] = new int[10], sum = 0, inuse = 5;
    
    // This code uses the full length of the array.
    for ( x = 0; x < ia.length; x++ ) {
      ia[x] = (int)(Math.random() * 100 + 1);
      sum = sum + ia[x];
    }
    
    System.out.println("The sum of random numbers is " + sum);
    System.out.println("The call to sum(ia) returns " + sum(ia));
    System.out.println("The call to sum(ia, 10) returns " + sum(ia, 10));
    
    /* This section uses only half the array and
     * demonstrates the need to keep the number
     * of elements in use.
     */
    sum = 0;
    
    for ( x = 0; x < inuse; x++ ) {
      ia[x] = (int)(Math.random() * 100 + 1);
      sum = sum + ia[x];
    }
    
    System.out.println("\nThe sum of random numbers is " + sum);
    System.out.println("The call to sum(ia) returns " + sum(ia));
    System.out.println("The call to sum(ia, inuse) returns " + sum(ia, inuse));

  }
}

Example 4: Overloaded sum().

Managing Arrays

public class UsingArrays2 {
  
  // Dump the array. Make it pretty.
  public static void dumpArray (int[] array) {
    
    int x, l = array.length;
    
    System.out.print("[ ");
    for ( x = 0 ; x < l - 1 ; x++ )
      System.out.print(array[x] + ", ");
      
    System.out.println(array[l-1] + " ]");

  }
  // Delete the number at pos.
  public static int delete(int[] array, int inuse, int pos) {
    
    /*
    
    Length is 9, in use is 9. If we call delete
    with pos 2, we loop from 2 to 7. This is due to 
    running off the end with x+1.
    
      0    1    2    3    4    5    6    7    8
     --------------------------------------------
    | 11 | 34 | 56 | -3 | 25 | 78 | 98 | 36 | 10 |
     --------------------------------------------
                 x   x+1                  x   x+1
                pos
                  BEGIN                    END
                  
                  
    Array after move. In use is now 8.
    
      0    1    2    3    4    5    6    7    8
     --------------------------------------------
    | 11 | 34 | -3 | 25 | 78 | 98 | 36 | 10 | 10 |
     --------------------------------------------

    */
    
    int x;
    
    for ( x = pos; x < inuse - 1; x++)
      array[x] = array[x+1];
      
    return inuse - 1;
  }
  
  // Insert val at pos.
  public static int insert(int[] array, int inuse, int pos, int val) {
    
    /*
    
    Length is 9, in use is 8. If we call insert
    with pos 3 and val 99, we loop from 7 to 3.
    This is due to running off the end with x+1.
    
      0    1    2    3    4    5    6    7    8
     --------------------------------------------
    | 11 | 34 | -3 | 25 | 78 | 98 | 36 | 10 | 0  |
     --------------------------------------------
                      x   x+1             x   x+1
                     pos
                       END                BEGIN

    Array after move with inuse at 9.
                  
      0    1    2    3    4    5    6    7    8
     --------------------------------------------
    | 11 | 34 | -3 | 99 | 25 | 78 | 98 | 36 | 10 |
     --------------------------------------------

    */

    int x;
    
    for ( x = inuse - 1; x >= pos; x--)
      array[x+1] = array[x];
      
    array[pos] = val;
    return inuse + 1;
  }
  
  public static void main(String[] args) {
  
    int x, ia[] = new int[10], inuse = ia.length;
    
    // Populate array with 10 random numbers
    for ( x = 0; x < ia.length; x++ )
      ia[x] = (int)(Math.random() * 100 + 1);
    
    System.out.println("Original array.");
    dumpArray(ia);
    System.out.println("\nDeleting at index 3.");
    inuse = delete(ia, inuse, 3);
    dumpArray(ia);
    System.out.println("\nInserting a zero at index 5.");
    inuse = insert(ia, inuse, 5, 0);
    dumpArray(ia);
  }
  
}

Example 5: First attempt at managing array contents.

Now one of the things that may not jump out immediately is the fact that there are no bounds checking being applied to this code. It was intentionally left out in order to focus on the logic of moving the array contents back and forth for closing and opening gaps as needed.

Now the next draft of the code introduces tighter restrictions on when work will be performed. It also introduces the idea of returning a -1 instead of the inuse value when a problem occurs.

And this is where the design begins to break down. This is where the ideas of encaposulation and literally hiding some of the details from the application writer become useful. Not because we wish to keep everyting a secret, but because the argument list the programming needs to provide it already getting long. The logic they need to maintain inside and outside the array management methods is becoming complicated and somewhat clumsy.

How? Well take a look at the rough and somewhat incomplete Example 6.

public class UsingArrays3 {
  
  // Dump the array. Make it pretty.
  public static void dumpArray (int[] array) {
    
    int x, l = array.length;
    
    System.out.print("[ ");
    for ( x = 0 ; x < l - 1 ; x++ )
      System.out.print(array[x] + ", ");
      
    System.out.println(array[l-1] + " ]");

  }
  // Delete the number at pos.
  public static int delete(int[] array, int inuse, int pos) {
    
    /*
    
    Length is 9, in use is 9. If we call delete
    with pos 2, we loop from 2 to 7. This is due to 
    running off the end with x+1.
    
      0    1    2    3    4    5    6    7    8
     --------------------------------------------
    | 11 | 34 | 56 | -3 | 25 | 78 | 98 | 36 | 10 |
     --------------------------------------------
                 x   x+1                  x   x+1
                pos
                  BEGIN                    END
                  
                  
    Array after move. In use is now 8.
    
      0    1    2    3    4    5    6    7    8
     --------------------------------------------
    | 11 | 34 | -3 | 25 | 78 | 98 | 36 | 10 | 10 |
     --------------------------------------------

    */
    
    int x;
    
    /* if pos is out of bounds or there are no 
     * items in the array, it is an error.
     */
    if ( pos > inuse || pos < 0 || inuse == 0 )
      return -1;
    
    // Note: if pos == inuse, no move happens.
    // Also, if pos == 0 and inuse == 1, 
    // no move happens.  
    for ( x = pos; x < inuse - 1; x++)
      array[x] = array[x+1];
      
    return inuse - 1;
  }
  
  // Insert val at pos.
  public static int insert(int[] array, int inuse, int pos, int val) {
    
    /*
    
    Length is 9, in use is 8. If we call insert
    with pos 4 and val 99, we loop from 7 to 4.
    This is due to running off the end with x+1.
    
      0    1    2    3    4    5    6    7    8
     --------------------------------------------
    | 11 | 34 | -3 | 25 | 78 | 98 | 36 | 10 | 0  |
     --------------------------------------------
                      x   x+1             x   x+1
                     pos
                       END                BEGIN

    Array after move with inuse at 9.
                  
      0    1    2    3    4    5    6    7    8
     --------------------------------------------
    | 11 | 34 | -3 | 99 | 25 | 78 | 98 | 36 | 10 |
     --------------------------------------------

    */

    int x;
    
    /* if the array is exhausted, cannot extend here.
     * You can add to one past inuse, but not past the end 
     * of the array.
     * If pos is out of bounds, it is an error.
     */
    if ( inuse == array.length || pos > inuse + 1
            || pos > array.length || pos < 0 )
      return -1;
    
    // Note: 
    for ( x = inuse - 1; x >= pos; x--)
      array[x+1] = array[x];
      
    array[pos] = val;
    return inuse + 1;
  }
  
  public static void main(String[] args) {
  
    int x, ia[] = new int[10], inuse = ia.length, result;
    
    // Populate array with 10 random numbers
    for ( x = 0; x < ia.length; x++ )
      ia[x] = (int)(Math.random() * 100 + 1);
    
    System.out.println("Original array.");
    dumpArray(ia);
    //System.out.println("\nDeleting at index 3.");
    //inuse = delete(ia, inuse, 3);
    //dumpArray(ia);
    System.out.println("\nInserting a zero at index 5.");
    result = insert(ia, inuse, 5, 0);
    if (result != -1 )
      inuse = result;
    dumpArray(ia);
  }
  
}

Example 6: A second draft of array management.

You can see there are many more if tests being applied to check the boundaries of the array and make sure we do not go too far above or below the range of indexes.

We have also commented out lines 114-116 to show what happens if we try to insert into a full array. It will fail and insert() will return -1. So, we have had to modify how we handle the return value. Lines 118-120 show how much more complicated the management of data within the array has become. Extra variables are now required to make sure we do not accidentally lose our current inuse value if a -1 gets returned.

Exercise 3 at the end of the chapter offers an opportunity to clean this up and put all of this management into a class to better serve the purposes of management and to provide a much better interface to the application writer who may take one look at this implementation and run for hills, screaming.

Quiz

Given:

public static int gr() {
  return (int)(Math.random()*100 + 1);
}

What is the output of the following:

y = gr();

 There is no output as there is no statement to produce output.

 A random number in the range 0 to 100.

 A random number in the range 0 to 99.

 A random number in the range 1 to 100.

What is wrong with the following method?

public static int sum(int a, int b) {

    return a + b;
}

 There is nothing wrong with this method.

 Only one int is required when defining the parameter list.

 You cannot have an expression in the return statement.

 Value returning methods cannot be static.

What is wrong with the following method?

public static void plen(String s) {

    return 2 * s.length();
}

 There is nothing wrong with this method.

 A void method cannot be static.

 The value of length() is not known to the method.

 A void method cannot return a value.

Given:

public static int gxt() {
  return (int)(Math.random()*20 + 1);
}

What is the output of the following:

System.out.println(gxt() + " " + gxt());

 Two random numbers, each in the range 1 to 20, with a space between them.

 Two random numbers, each in the range 0 to 20, with a space between them.

 The sum of two random numbers, each in the range 0 to 20.

 The sum of two random numbers, each in the range 1 to 20.

Are the following allowed to be overloaded by the compiler?

public static String xp(int x, double y) {...}
public static double yp(int a, double b) {...}

 No. Differing return types must have the same parameter list.

 No. The have the same signature.

 No. They must have the same return type.

 These are not overloaded methods.

Are the following allowed to be overloaded by the compiler?

public static int  cp(int x, int y) {...}
public static long cp(long a, long b) {...}

 No. Differing return types must have the same parameter list.

 Yes. Everything is declared correctly.

 No. They must have the same return type.

 No. The have the same signature.

Are the following allowed to be overloaded by the compiler?

public static String cp(int x, double y) {...}
public static double cp(int a, double b) {...}

 No. They must have the same return type.

 No. The have the same signature.

 No. Differing return types must have the same parameter list.

 Yes. Everything is declared correctly.

Given:

public static String comp(int x, double y, char c) {
	//...
}

What is the signature of comp()?

 String comp()

 comp(int, double, char)

 comp()

 String comp(int, double, char)

Overloaded methods must differ in

 name.

 return type.

 static versus non-static.

 number or type.

 Loading …

Question 1 of 9

Exercises

1. (Beginner) Populate a single-dimension, 25-element integer array with random values. Using the array in a single loop, display the values as an evenly spaced 5x5 grid.
2. (Intermediate) As proof, demonstrate the incorrect way to represent opening and closing space in an array (Example 5). Display to arrays before and after in both instances to witness the damage done. (You may use a similar 10-element array partially populated and simulate in a single what the insert() and delete() methods do or write the complete methods both ways.)
3. (Advanced) Fix Example 6 implementing a user-defined class to manage the array and the inuse value. Transform the methods to be aware of the class and adjust the parameters accordingly. You may want to create an add() method to add a value on the end of the array as well as a get() method to return a value at a given location. Once you write get(), you will see the issues that can be addressed with exceptions. (There are a few ways to tackle this, so your code may look slightly different than the solution.)