(Updated January 10, 2026)
Table of contents
-
Overview
The Basics
An Example
Different Types of Recursion
Another Example
The Cost
Memoization
Exercises
Overview
We have previously determined that we often need to do some work while a condition exists or until a condition is met. This has always been handled using an iterative process, which we call a loop. There can be some cases, however, where the use of a loop may not be straightforward or is otherwise complicated by the logic or the data structure in use.
Recursion is essentially iterative in its design but uses a different component for control – specifically, the runtime call stack. Recursion has its roots in the Lambda calculus and is the core of functional programming – both topics are well beyond the scope of this discourse.
When we use a loop, we often refer to a loop-control variable.
int x;
for (x = 0; x < 10; x++)
printf("%d\n", x);
In the code above, the loop control variable is x and will be used to determine when the loop will stop based on the condition. The variable x is likely a local variable, meaning the scope is local to the function in which it is defined. Local variables are also called automatic variables. This means they are automatically created with each function's call; hence, each function call gets its own set of local/automatic variables.
Automatic (local) variables are created on the runtime stack (along with the argument data passed to the function) and are thrown away when the call is complete. Each call to a function is separate, with a distinct set of arguments and local variables. Each invocation is then locked in time to allow other work (subsequent calls to the same function) to proceed. When control returns to a previous time-locked call, the results from the other calls can be used to influence (or not) the work that remains to be completed.
The call stack becomes part of the control since each function call contains point-in-time knowledge of how the problem-solving process is progressing. As this big-picture view is often necessary to solve more significant problems, there may be a need for more than just a simple loop-control variable.
This is the key to recursion.
The Basics
With recursion, there is a predisposition that the function will invoke itself either directly or indirectly. In other words, the function may explicitly call itself (direct) or another function that will then call this function again (indirect).
Since the function will be asked to invoke itself again before the current call is completed, we need a mechanism to stop this. So we need a set of cases to assist with call control:
- The base case is the case under which all additional calls will occur.
- The stopping case is the case under which we make sure no more calls occur. This begins the process of unraveling the call stack and allows the previous calls to complete.
An Example
Consider the obligatory Factorial calculation such that 4! = 24 (4*3*2*1) and 0! = 1. This is the simplest calculation in both iterative and recursive solutions. This is due to the sheer simplicity of the algorithm and why it is so popular to illustrate recursion and is shamelessly repeated here. The code in Example 1 illustrates the iterative approach.
#include <stdio.h>
#include <errno.h>
int fact(int n) {
int prod = 1;
if (n < 0) {
errno = EINVAL;
return -1;
}
for (int i = n; i > 1; i--)
prod = prod * i;
return prod;
}
int main(int argc, char **argv) {
printf("%d\n", fact(0));
printf("%d\n", fact(4));
printf("%d\n", fact(15));
return 0;
}
Example 1: Factorial through iteration.
The product of the reducing values of n is set to 1 to cover the 0! possibility. Otherwise, we count down from the start until we reach 1 and return the result. Simple. Now consider the version in Example 2 as an alternative solution using recursion.
#include <stdio.h>
#include <errno.h>
int fact(int n) {
if (n < 0) {
errno = EINVAL;
return -1;
}
if (n == 0 || n == 1)
return 1;
else
return n * fact(n - 1);
}
int main(void) {
printf("%d\n", fact(0));
printf("%d\n", fact(4));
printf("%d\n", fact(15));
return 0;
}
Example 2: Factorial using recursion
We are still reducing the value of n, but in this case, it is done with each subsequent call to fact(). So each call will end up calling itself with a smaller value of n. That is, until n reaches one of the stopping cases of being 0 or 1.
Now is a good time to reiterate that a recursive function comprises both a base case and a stopping case. The base case is used when we know another call must be made, and the stopping case causes the calls to stop - in fact, it causes all previous calls to complete in the reverse order in which they were invoked. This is because the call stack has return addresses of who called placed at the top each time. All we do now is allow the calls to return, and the values are sent back to the original callers as the stack unwinds.
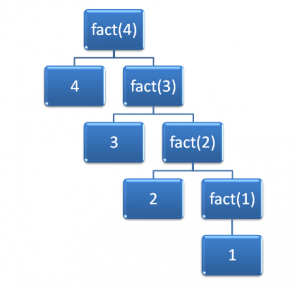
Figure 1: Values calculated with each call to fact().
Figure 1 shows the calls occurring as a tree. This was done to demonstrate that for each call that is made to fact(), there are two parts:
- The current value of n.
- The next call.
With multiplication implied on each row of the tree, it should be easy to see how, in the final row, the value 1 (stopping case applied) is returned up the call tree so that we end up with 2*1 returned, which results in 3*2 returned which results in 4*6 as the final value returned to fact(4).
Different Types of Recursion
There are fundamentally two major forms of recursion:
- Direct - Function always calls itself. (FunctionA -> FunctionA -> FunctionA ...)
- Indirect - Function calls one or more partner functions which eventually end up circling back to calling the original. (FunctionA -> FunctionB -> FunctionC -> FunctionA ...)
There are four different types of direct recursion:
- Tail - performs other work before calling itself (at the tail end of the work).
- Head - calls itself (at the head end of the work) before doing anything else.
- Linear - this refers to code that only calls itself once in the body of the recursion.
- Tree - calls itself at least twice within the body of the recursion.
Now, let us discuss the differences here. The code in Example 2 is direct, linear tail recursion. Of course, we could move a few things around and make it head recursion:
int fact(int n) {
if ( n > 1 )
return fact(n-1) * n;
else if (n == 0 || n == 1)
return 1;
else {
errno = EINVAL;
return -1;
}
All we did was move where the recursive portion happens. Subsequently, we flipped the tree such that the calls now run down the left-hand side.
In the next section, we will look at tree recursion in detail.
Another Example
Consider both the iterative and recursive options of any given solution. If something is difficult to write for one or the other, then the path is likely undeniable as to what you should choose.
If something can be written relatively simply, both iteratively and recursively, begin by evaluating the number of resources it would take to complete the task for each model.
Consider the fundamental Fibonacci (golden ratio) sequence:
- Start with 0 and 1 as the first two numbers.
- To compute the third, you sum the first and second.
- To compute the forth, you sum the second and third. And so on.
The first 47 Fibonacci numbers are:
0 1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 987 1597 2584 4181 6765 10946 17711 28657 46368 75025 121393 196418 317811 514229 832040 1346269 2178309 3524578 5702887 9227465 14930352 24157817 39088169 63245986 102334155 165580141 267914296 433494437 701408733 1134903170 1836311903
The computing of the next value would overflow a 32-bit integer, so a long would need to be considered for higher Fibonacci sequences.
The Fibonacci function is written such that F(0) = 0, F(1) = 1, F(2) = 1, F(3) = 2, ..., F(46) = 1836311903.
Now an iterative program looks like this:
#include <stdio.h>
#include <errno.h>
int fib(int n) {
if (n < 0) {
errno = EINVAL;
return -1;
}
int previous = -1;
int current = 1;
for (int i = 0; i <= n; i++) {
int sum = current + previous;
previous = current;
current = sum;
}
return current;
}
int main(void) {
printf("%d\n", fib(46));
return 0;
}
Example 3: Fibonacci as an iterative solution.
And a recursive one looks like:
#include <stdio.h>
#include <errno.h>
int fib(int n) {
if (n < 0) {
errno = EINVAL;
return -1;
}
if (n == 0 || n == 1)
return n;
return fib(n - 1) + fib(n - 2);
}
int main(void) {
printf("%d\n", fib(46));
return 0;
}
Example 4: Fibonacci as a recursive solution.
The iterative approach is relatively straightforward and follows the rules we established earlier. The previous and current numbers are used with each iteration to compute a third. The numbers are then arranged such that the current becomes the previous, and the newly calculated one becomes the current. We continue until the correct number of iterations has occurred, then return the value.
The recursive version uses the ability of a function to call itself and uses the founded premise that we are summing the previous two Fibonacci numbers to calculate our own; therefore, it seems logical that we would add the invocations of the two values before our own, namely n-1 and n-2.
The problem is that although this seems rather logical, we have introduced one of the most poorly crafted recursive functions! For any call to be complete, it must successfully make two additional calls. Going further, the calls must eventually end where n==0 or n==1.
So, if we were to picture what a call to fib(4) might look like with all the additional calls being made, you might see it pictured as something like Figure 2.
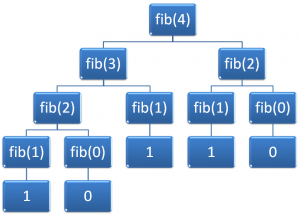
Figure 2: Hierarchy of calls made for fib(4).
This means that a total of 5 values will be summed, and there were 9 calls made. So to calculate this, we needed to make 9 calls compared to 5 iterations for the iterative equivalent. This means we should investigate further the amount of work required to complete the job.
Now here is the recurseFib.c with an additional recording of the number of calls made to fib().
#include <stdio.h>
#include <errno.h>
long fibcalls;
int fib(int n) {
fibcalls++;
if (n < 0) {
errno = EINVAL;
return -1;
}
if (n == 0 || n == 1)
return n;
return fib(n - 1) + fib(n - 2);
}
int main(int argc, char **argv) {
fibcalls = 0;
printf("%d\n", fib(1));
printf("fibcalls = %ld\n", fibcalls);
fibcalls = 0;
printf("%d\n", fib(4));
printf("fibcalls = %ld\n", fibcalls);
fibcalls = 0;
printf("%d\n", fib(46));
printf("fibcalls = %ld\n", fibcalls);
return 0;
}
Example 5: Fibonacci as a recursive solution with additional code to count the number of calls.
Additionally, we are testing fib(1), fib(4) and fib(46). The output of the above is as follows:
1 fibcalls = 1 3 fibcalls = 9 1836311903 fibcalls = 5942430145
The amount of work necessary to calculate Fibonacci numbers recursively is not paying off. Of course, this is because each call made will result in two more.
From a Big-O perspective, this could be perceived as linear, meaning that we know that there will be about three times as many calls as the value we are searching for in a given Fibonacci slot. The reality is that it is much, much worse. To find the 47th number, we need to make nearly 6 billion function calls. That isn't very good.
So, let's try one more time. We've introduced a second function that is private and can only be invoked by fib().
There are two variables p (previous) and c (current). The fib() function calls fib2() with values of n, -1 and 1. The value of n still represents the Fibonacci number we seek. The -1 is the previous value (we have not seen any yet) and 1 is the current. One need only look over the iterative version, above, to understand what has been done. We have simply used recursion to implement the iterative properties of the first example.
#include <stdio.h>
// prototypes
int fib(int n);
int fib2(int n, int p, int c);
// global
long fibcalls;
int fib(int n) {
return fib2(n, -1, 1);
}
int fib2(int n, int p, int c) {
fibcalls++;
if (n == 0)
return p + c;
return fib2(n - 1, c, p + c);
}
int main(void) {
fibcalls = 0;
printf("%d\n", fib(46));
printf("fibcalls = %ld\n", fibcalls);
return 0;
}
Example 6: Refactored Fibonacci recursive solution.
Although this code addresses the performance issue, it reveals that sometimes the iterative approach is possibly the better one due to the simplicity of the solution. You can see that the number of calls has been dramatically reduced.
1836311903 fibcalls = 47
The Cost
If you have not already done so, review the Big-O Notation write-up.
We mentioned Big-O earlier as a means to put some code into perspective. Now we will delve into the details of time and space complexity concerning iterative and recursive solutions.
| Example | Time Complexity | Space Complexity | Comment |
|---|---|---|---|
| Iterative factorial | O(n) | O(1) | Linear operations while space remains constant. |
| Recursive factorial | O(n) | O(n) | Linear operations, and we incur space on that stack with each call making it linear as well. |
| Iterative Fibonacci | O(n) | O(1) | Linear operation while space remains constant. |
| Recursive Fibonacci | O(2n) | O(2n) | This is tree recursive, and seeking value 46 yields 6B calls and significant memory usage. |
| Improved recursive Fibonacci | O(n) | O(n) | By refactoring the code, we reduce the number of calls. |
| Memoized recursive Fibonacci (See below) | O(1) | O(n) | By introducing a new data structure, we reduce the number of calls and memory usage. |
Table 2: Example work with the time and space complexity.
There is a stark difference between the implementations of Factorial and Fibonacci. The Factorial solution is linear regardless of whether we choose iterative or recursive. That is to say that the number of calls in the recursive method equals the number of times through the loop in the iterative solution. At that point, it would be a question of which solution is faster and easier to maintain.
The takeaway is that, if nothing else, we need to be mindful that we can approach a problem from both the iterative and recursive perspectives. Just make sure that the cost of your choice is worth the investment.
If the recursive solution is elusive, it likely is that one does not exist directly or may be very complicated to implement. This means you may have to refactor how you are approaching the solution. See the Tree code for examples of how things may need to be refactored.
As a final note, consider this: become acquainted with binary trees, particularly the pre-, in-, and post-order processing that is done recursively. Now try to find an iterative solution to that problem.
Need a hint? A stack will allow you to keep track of items visited but not ready to be printed due to your location in the tree. You store values on the stack as you loop through the left and right sub-trees.
Memoization
In trying to improve algorithms where iteration cannot be applied, there are other ways to enhance recursive situations with no solution other than tree recursion. In these situations, we can rely on knowledge we have already obtained.
Memoization is not new and was first coined in the late 1960s by Donald Michie. It is from the Latin memorandum. A memorandum was also an instrument in early office culture whereby letters were sent to people highlighting important details not to be forgotten. This was also often expressed as a memo.
So, memoization is a collection of things we should not forget since we have already spent the capital on obtaining the knowledge.
#include <stdio.h>
// globals
long fibcalls;
#define MEMO_SIZE 100
int memo[MEMO_SIZE];
int fib(int n) {
fibcalls++;
if (memo[n] != -1)
return memo[n];
if (n == 0 || n == 1)
return n;
int sum = fib(n - 1) + fib(n - 2);
memo[n] = sum;
return sum;
}
int main(void) {
// allocate array and set start values to -1.
for (int x = 0; x < MEMO_SIZE; x++)
memo[x] = -1;
fibcalls = 0;
printf("%d\n", fib(46));
printf("fibcalls = %ld\n", fibcalls);
return 0;
}
Example 7: Fibonacci recursive memoization solution.
The code in Example 7 uses an array solution. The index is the Fibonacci sequence number we seek, and the value contained in the array is that value.
We begin by creating a brand new array initialized to -1, and then begin the calculations for Fibonacci numbers. Along the way, we can ask if we've seen it before by checking for -1. If it's non-negative, we've seen it before, and if it is -1, we replace it with the newly discovered numbers.
The program proceeds along these lines such that we do not waste time computing numbers we already know - we look them up.
Remember that this is only a demonstration of how we can use another tool the solve the problem of helping highly compute-intensive algorithms be more efficient. In practical design, we would not use a model such as this to keep track of a few Fibonacci numbers. However, you can see the power of such an approach and the freedom it offers the programming to keep moving forward.
This is still a significant reduction in the number of calls and is perfect to use when the code is too complicated to consider refactoring.
1836311903 fibcalls = 91
Take a moment to review the time and space complexity for this solution noted in Table 2.